Searching Algorithms - A Review

Searching

The need to find a specific item in a collection of items is a very common problem in computer science. Often, a large collection of data will need to be sifted through in order to find an exact element.

Linear Search

A naive approach to finding a specific element in a list of elements is to look at each element in the list and check if that element is equal to the element we are trying to find. If it is, we'll return the index. If the element cannot be found in the list, we can simply return -1.

This could be implemented follows:

public class Search {

    public static void main(String[] args) {
        int[] list = { 3, 4, 2 , 7, 1, 9, 5, 6, 12, 34 };
        int index = linearSearch(9, list);
        System.out.println("The item is at index: " + index);
    }

    private static int linearSearch(int itemToFind; int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == itemToFind) {
                return i;
            }
        }
        return -1;
    }

}

For our list of numbers { 3, 4, 2, 7, 1, 9, 5, 6, 12, 34 } our algortihm would return 5 since 9 is at the 5th index in the list.

But how efficient is our algorithm? In our case, it took 6 iterations of the for loop to find the element 9. What if the element we were searching for was 34? In that case, we would execute 9 iterations of the for loop before finding the element--equivalent to the size of the input list.

This algorithm then has a runtime complexity of O(n) where n is the size of the input list. This is an okay runtime, but if the list was 1,000,000 items long it could take some time to find the item we need. Can we do better?

What if the given input array was gauranteed to be sorted?

If we were gauranteed to have a sorted list could we use the characteristcs to improve our searching algorithm. Well, indeed we can.

If we know that the input array is sorted we can look at the element in the middle of the list and compare it to the element that we are searching for. If the element we're searching for is less than the middle element, then it must be on the left-hand side of the list. If it's greater, than it must be on the right. We can continue this process, drilling down into the left or right side of the list, until we find out element.

Below is a representation of binary search vs. linear search:

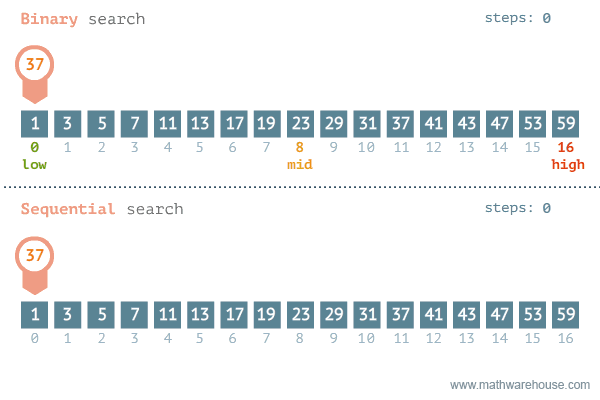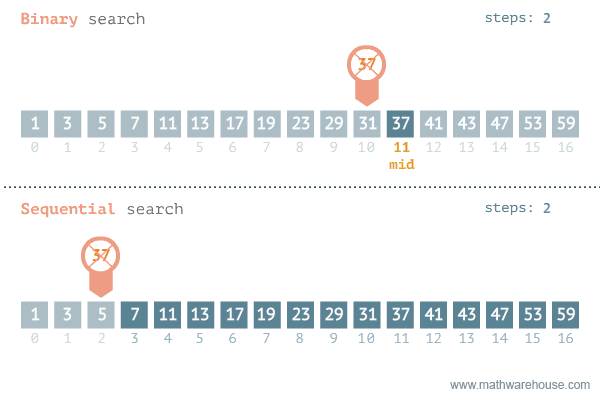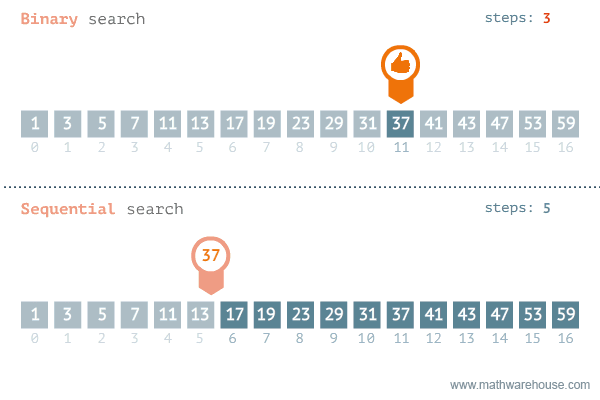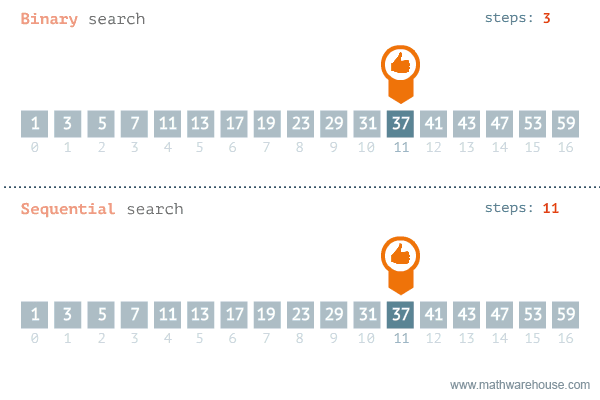
Can you start to see how this might be implemented?

Binary Search

Below I've implemented binary search for our use case.

public class Search {
    public static void main(String[] args) {
        int[] sorted = { 1, 3, 7, 18, 29, 31, 42, 43, 57, 63, 70 };
        int index = binarySearch(42, sorted);
        System.out.println("The answer is: " + index);
    }

    private static int binarySearch(int itemToFind, int[] arr) {
        if (arr.length == 0) return -1;
        if (arr.length == 1) {
            return arr[0] == itemToFind
                ? 0
                : -1;
        }
        
        int start = 0;
        int end = arr.length - 1;
        return binarySearch(itemToFind, arr, start, end);
    }

    private static int binarySearch(int itemToFind, int[] arr, int start, int end) {
        System.out.println("start: " + start + ", End: " + end);
        if (start >= end) { 
            return -1;
        } 

        int middle = ((end - start) / 2) + start;
        int middleItem = arr[middle];

        if (itemToFind < middleItem) {
            return binarySearch(itemToFind, arr, start, middle - 1);
        } else if (itemToFind > middleItem) {
            return binarySearch(itemToFind, arr, middle + 1, end);
        } else {
            return middle;
        }
    }
}

Note that we uses a recursive helper method to implement binary search. With the given input array and the item to find we call a method that takes a start and end index in our list. This method fits the signature of a method that can be called recursivly on the left or right sub-lists as we compare our item to find with the middle element

Also notice the constraint that we have to check against in the recusive method. If our start index is greater than or equal to our end, then we know that we've gotten to a point in our recursive stack such that the item we're trying to find can't exist in the list. Thus, our algorithm will return -1 to indicate that the item is not in the list. Without this constraint check, our algorithm would end up recursing indefinitely.

Finally, to handle the edge cases where our input list could be empty or only containing a single element, we can but some conditionals at the beginning of our implementation to catch these cases and respond quickly. If the array is empty, we know the item to find cannot be in the list. If the array has only one element, we can simply check if that one element is the element we're trying to find. If so, we'll return the index 0, if not, we'll return -1.

This binary search algorithm will find our item in a worst-case time complexity of O(log(n))--much better than the linear search algorithm.

Sorting

Great, we've come up with a quick search algorithm. But wait a minute, we made some assumptions about our list to get here. For binary search to work, we need a sorted list. How do we get from an unordered list to an ordered list? And is sorting a list and then searching for an element really faster than the intuitive linear search of an unordered list?

The short answer is yes. To find out why, check out my next article Sorting - A Review